Caro(a)s leitore(a)s, bom estar de volta! Um momento de contemplação e… mãos à obra!
Nada melhor do que começar com uma pequena festa. Nessa celebração matemática, Alberto e Alberta recebem quatro casais de amigos, formando um grupo de 10 pessoas.
O perspicaz Alberto nota uma particularidade: os convidados e Alberta apertaram as mãos, de maneira que o número de mãos que cada um apertou difere para cada um deles. Repare que alguns deles podem ter apertado a mão de Alberto. Além disso: i) ninguém apertou a própria mão (faz sentido!); ii) os casais não apertaram as mãos entre si (faz sentido?).
Pergunta: quantas mãos Alberta apertou?
Parece haver pouca informação para resolver esse problema… Mas vejamos o que pode ser feito.
Como são oito convidados, temos, contando com Alberta, nove pessoas. Uma primeira observação simples: o número de apertos de mão que cada pessoa deu tem que, necessariamente, variar entre 0 – não apertou a mão de ninguém – e oito ‒ apertou a mão de todos, exceto o(a) parceiro(a). Total de possibilidades: nove.
Como o número de apertos de mãos difere de pessoa para pessoa, alguém, obrigatoriamente, não terá apertado a mão de ninguém (‘o(a) antissocial’), e haverá aquele(a) que apertou uma vez; o(a) que apertou duas… Até a pessoa (‘o(a) popular’) que deu oito apertos de mão.
Como o(a) popular não apertou a mão do(a) próprio(a) parceiro(a), ele(a) tem que ter apertado a mão de todas as outras pessoas, para chegar ao total de oito apertos. Isso significa que cada um dos outros (além do parceiro do(a) popular) apertou a mão de pelo menos uma pessoa.
Quem pode ter apertado zero mão, então? A única possibilidade é o(a) parceiro(a) do(a) popular!
Resumindo: há um casal no qual um deles apertou a mão de oito pessoas, e o outro não apertou a mão de ninguém. Ou seja, popular e antissocial.
Podemos continuar com essa estratégia de análise, criando uma ‘subfesta’ (com as mesmas regras), na qual não está mais o casal ‘popular e antissocial’. Excetuando-se Alberto, ficarão sete pessoas, cada uma destas tendo dado um número de apertos que varia de zero a seis. Aplicando o mesmo raciocínio, vemos que a pessoa que apertou seis mãos nessa subfesta é parceira daquela que não cumprimentou ninguém.
Portanto, temos o seguinte cenário para a festa com as nove pessoas: quem apertou a mão de oito pessoas é parceiro(a) de quem apertou zero mão; quem apertou sete forma casal com quem apertou uma mão, e assim por diante. Há um padrão: cada casal sempre soma oito apertos.
Mas sobra um número: quem apertou quatro mãos?
A resposta só pode ser uma pessoa que não faz parte de nenhum dos casais convidados… Alberta! O porquê de ser ela é que… bem, caro(a) leitor(a), veja o nosso bom e velho desafio.
Pode parecer surpreendente que, com tão pouca informação, tenhamos chegado a uma conclusão tão específica. Porém, não sabemos que mãos Alberta e seus convidados apertaram. A matemática não nos permite saber tudo que aconteceu. Mas de uma coisa temos certeza: essa festa matemática foi muito divertida!
Solução do desafio passado
O efeito de o ajudante número 99 ter faltado é o mesmo de ele ter passado duas vezes: se a porta estava fechada (aberta), ele passa uma vez e abre (fecha); numa segunda vez, ele fecha (abre), voltando ao estado inicial. Como ele só havia mexido na porta 99, que terminou fechada, se ele faltou, a porta termina aberta. Portanto, as portas abertas nesse caso são 1, 4, 9, 16, 25, 36, 49, 64, 81, 99 e 100.
Marco Moriconi
Instituto de Física
Universidade Federal Fluminense
Está mesmo ocorrendo um aquecimento em todo o planeta? Existe alguma relação entre as vacinas e a ocorrência de autismo? Há evidências de que os neandertais acasalaram com os humanos modernos? Confira as respostas de especialistas.
As descobertas recentes do bóson de Higgs e das ondas gravitacionais, que deram veracidade a duas grandes teorias físicas, guardam entre si uma grande incompatibilidade. Essa divergênciaocorre desde a construção das bases dessas teorias, há cerca de um século, e reflete um conflito histórico entre célebres cientistas queserviu como motor do desenvolvimento científico.
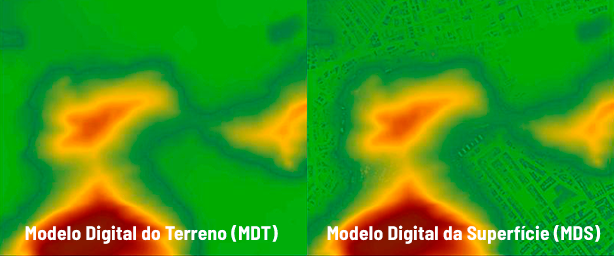
Cidades antigas escondidas, cavernas escuras, áreas de florestas fechadas, estrutura de prédios históricos. O sistema LiDAR, tecnologia de varredura a laser, descortina um mundo que estava escondido de nossa visão, com aplicações que vão do planejamento urbano à preservação florestal.
Natal. E Noel veio... de novo – claro, com Günther, o comilão. Mais uma vez, nada de presentes do ‘bom velhinho’, mas ele, como sempre, deixou um desafio interessante escrito em um papelzinho: uma sequência de letras que devem formar pares entre si
A matemática pode ser uma ferramenta útil também no mercado editorial. Nesta coluna, veremos como a teoria das probabilidades pode nos ajudar a quantificar as chances de dois revisores de uma editora, trabalhando de forma independente, encontrarem erros de digitação nas provas de um livro
Com só uma regra simples, denominada ‘condição de neutralidade’, um joguinho fácil, divertido e instrutivo – para o qual você só precisa de uma folha de papel e quatro canetinhas de cores diferentes – vai te revelar uma surpreendente propriedade sobre tabuleiros coloridos
Um problema que pode ser simulado com elásticos e preguinhos sobre uma tábua de madeira não é só interessante, instrutivo e divertido, mas também tem papel de destaque na história da matemática, pois sua resolução tem algo dos roteiros de filmes românticos
Duas irmãs e duas amigas delas. Todas as quatro excelentes tenistas. Elas decidem disputar, entre elas, um torneio do tipo ‘perdeu, tá fora’. Qual a probabilidade de as duas irmãs se enfrentarem? Soa complicado. Mas a matemática está aí para simplificar as coisas
Uma intoxicação atinge amigos em um acampamento. No hospital, o médico de plantão enfrenta problema sério: como dar a cada paciente o maior número possível de doses de uma vacina (sem exceder o limite seguro), quando os três tipos de imunizante vieram sem rótulos?
Claro, Noel e seu ‘simpático’ ajudante, Gunther, apareceram. Desta vez, abriram presentes, comeram bolo e usaram – para variar – um truque ‘desleal’: apresentaram ao dono da casa um problema fácil para, depois, complicar as coisas. Mas, no fim, foi divertido
Seguimos com o joguinho popular cujo desafio é encontrar rapidamente figuras em comum entre duas cartas. Neste mês, exploraremos questões intrigantes e ainda desafiadoras para a matemática: dado certo número de figuras, quantas cartas terá nosso jogo?
Um joguinho popular – cujo desafio é encontrar rapidamente figuras em comum entre duas cartas – está baseado em conceitos ‘ocultos’ de uma área da matemática: a geometria projetiva finita, que lida basicamente com pontos e linhas que se cruzam
Uma reflexão (mental) sobre os espelhos nos revelará que esses objetos escondem ‘mistérios’ não só interessantes, mas também úteis – tanto aqui na Terra quanto no espaço. Depois de ler esta coluna, você terá outra imagem sobre essas superfícies refletoras.
