É possível trabalhar problemas de otimização combinatória na educação básica? A seção “Mulheres na ciência” publicada na edição 411 da CIÊNCIA HOJE e intitulada “Em busca de soluções” destaca a trajetória da professora e cientista Carla Negri Lintzmayer por meio de um relato autobiográfico em que a autora declara sua afinidade pela Matemática, ainda que tenha escolhido a Ciência da Computação para formação acadêmica. 

Em seu cotidiano, a pesquisadora lida com problemas de otimização combinatória, em busca da melhor solução dentre todas as possibilidades. No contexto do ensino médio, exploramos a diversidade de soluções que problemas de combinatória de contagem possibilitam através da utilização de recursos como diagramas de árvores, tabelas de dupla-entrada, desenhos, multiplicação, fórmulas, entre outros.  Neste sentido, indicamos uma proposta pedagógica para aulas de matemática, buscando introduzir o conceito de permutação com repetição a partir de um problema de otimização combinatória.

Esta proposta é, idealmente, indicada para introduzir o conceito de permutação com repetição em turmas de 2ª série do Ensino Médio, sendo possível adaptá-la para outras séries desde que conceitos prévios, como os do princípio multiplicativo, de permutações simples e de combinações simples tenham sido abordados. 

Recomenda-se que a aula seja iniciada com a proposta da leitura do texto “Em busca de soluções”, da seção “Mulheres na ciência” publicada em CH 411, que deve ser disponibilizado em formato impresso ou digital. Em seguida, solicite que os estudantes selecionem trechos e fatos que mais chamaram a atenção deles na leitura do texto. 

Na sequência, proponha um debate a partir do que foi selecionado, buscando destacar principalmente: (i) a representatividade de mulheres na ciência e a necessidade de persistência dos jovens universitários na área acadêmica em busca de soluções concretas da vida real; (ii) o que é a ciência da computação e como ela pode se relacionar com a matemática, sobretudo através dos algoritmos; (iii) o que significa o termo otimização; (iv) a existência de problemas de combinatória, como os de otimização, que não se referem apenas à contagem.

Posteriormente, recomenda-se a apresentação do vídeo “Qual o melhor caminho?” (link no item “Recursos utilizados”). Nesta produção, apresenta-se um contexto em que um motoboy necessita entregar uma encomenda em duas horas e, para isso, necessita achar o melhor caminho para chegar ao local, a cidade de Rio Claro, no interior de São Paulo – cidade com vias em traçados retilíneos. Ele pede ajuda à atendente que solicitou o serviço e ela o orienta indicando que o melhor caminho é o mais curto. 

Neste diálogo, o motoboy pergunta: “qual é o melhor caminho?”. Em seguida, a atendente explora o mapa da cidade e traça eixos cartesianos para representar os dois pontos que interessam ao motoboy: o de partida e o de chegada. Recomenda-se que o(a) professor(a) pause o vídeo no instante 2:52 e pergunte aos estudantes quantas são todas as possibilidades de fazer o caminho do motoboy, independentemente do total percorrido, considerando apenas a possibilidade de andar na horizontal e na vertical, em vias de mão dupla. 

Em seguida, questione os estudantes sobre formas de otimizar este caminho, indicando quantas são as possibilidades de otimização, isto é, quantas são as possibilidades de fazer o menor caminho entre os dois pontos. Estas duas perguntas evidenciam o significado do termo otimização na prática e estimulam os estudantes a resolverem o problema utilizando apenas ferramentas já conhecidas, como a listagem de possibilidades, por exemplo. 

Depois desse momento, retome o vídeo para apresentar a solução, em que a atendente utiliza anagramas, introduzindo o conceito de permutação com repetição.

Por fim, recomenda-se a leitura da questão a seguir, presente no Exame Nacional do Ensino Médio (Enem) e que versa sobre combinatória:

QUESTÃO (ENEM 2020)

Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.

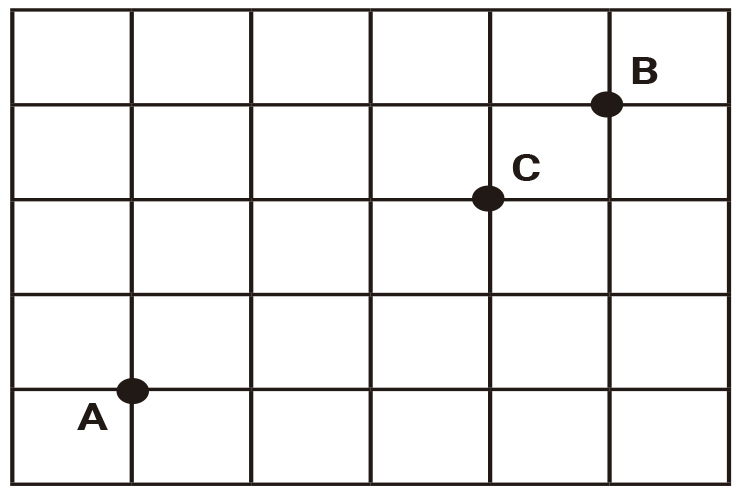
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita (→) ou para cima (↑), segundo o esquema da figura.

O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é

4. A) 4.
5. B) 14.
6. C) 17.
7. D) 35.
8. E) 48.

Após a resolução da questão por parte dos estudantes, apure quantos deles escolheram cada uma das alternativas, indique a correta (letra C) a partir de uma resolução comentada e promova, em seguida, um debate a partir da seguinte pergunta:

PERGUNTA: Como vocês acreditam que são escolhidos os valores que figuram nas alternativas erradas dessa questão do ENEM?

A ideia, nessa ocasião, não é apenas realizar a simulação da realização de uma prova, mas também de mostrar que os erros esperados em questões de matemática estão presentes na elaboração delas.