Colaboração: Leo Akio Yokoyama (CAp/UFRJ)
As aulas de matemática na educação básica podem abordar música clássica, neurônios e flocos de neve? O artigo A matemática e a arte dos fractais da edição 397 mostra que sim, é possível e destaca as estruturas geométricas que têm como característica a capacidade de se repetir indefinidamente. Isto é, no objeto geométrico em questão, é possível visualizar cópias da sua versão original em pedaços de tamanhos tão pequenos quanto se queira. Tais estruturas geométricas podem ser vistas e produzidas nos mais diversos contextos e se relacionam não só com a geometria, mas também com sequências, sejam elas pictóricas ou numéricas. Assim, apresentamos aqui uma proposta pedagógica para aulas de matemática buscando relacionar os fractais com o ensino de sequências.
Esta proposta é indicada para turmas da 1ª série do ensino médio, sendo possível adaptá-la para outras séries e contextos. Recomenda-se que o texto do artigo A matemática e a arte dos fractais seja disponibilizado e lido anteriormente pelos estudantes, preferencialmente como tarefa domiciliar. Além disso, que os temas “sequências” e “progressões geométricas” já tenham sido apresentados aos estudantes. Nos primeiros minutos de aula, indica-se que sejam estimulados os comentários dos estudantes em relação ao texto lido e, principalmente, sobre as imagens presentes no artigo.
Após o debate do texto, recomenda-se a leitura da questão a seguir, presente no Exame Nacional do Ensino Médio (Enem) e que versa sobre uma estrutura geométrica construída a partir de uma recursividade:
(Enem, 2020) O artista gráfico holandês Maurits Cornelis Escher criou belíssimas obras nas quais as imagens se repetiam, com diferentes tamanhos, induzindo ao raciocínio de repetição infinita das imagens. Inspirado por ele, um artista fez um rascunho de uma obra na qual propunha a ideia de construção de uma sequência de infinitos quadrados, cada vez menores, uns sob os outros, conforme indicado na figura.
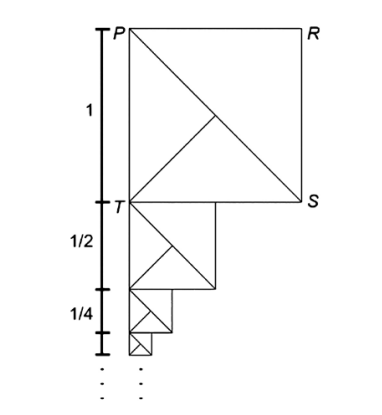
O quadrado PRST, com lado de medida 1, é o ponto de partida. O segundo quadrado é construído sob ele tomando-se o ponto médio da base do quadrado anterior e criando-se um quadrado novo, cujo lado corresponde à metade dessa base. Essa sequência de construção se repete recursivamente. Qual é a medida do lado do centésimo quadrado construído de acordo com esse padrão?
Em seguida, antes de propor que os estudantes resolvam a questão, promova um debate a partir das seguintes perguntas:
Após esse momento, retome a questão do Enem e incentive que cada estudante elabore a sua resolução. Caso seja necessário, relembre as principais características, propriedades e resultados que auxiliam no processo de solução da questão. A ideia, nessa ocasião, não é estimular uma simulação da realização da prova, mas, sim, mostrar que algumas questões de matemática podem versar sobre, ou ter como contexto, outras áreas do conhecimento. Ao final, solicite que os estudantes se manifestem em relação às respostas que deram e, em seguida, apresente uma solução correta, indicando que esta é a forma escolhida por você, professor(a), não a única que leva à resposta correta.
Por fim, recomenda-se que os estudantes, em grupos de 4 ou 5 componentes, pesquisem sobre a relação do trabalho do artista plástico Escher com a matemática. Tal pesquisa pode se configurar em um trabalho mais amplo que tenha a interdisciplinaridade entre as Artes e a Matemática como foco.
Soma de Progressão Geométrica. Pré-Vestibular CEDERJ. Disponível em https://www.youtube.com/watch?v=fRKt4BWJX7E
Arte e Matemática. NÚMEROS E FUNÇÕES. Série Matemática na escola, M3 Matemática Multimídia, UNICAMP. Disponível em: https://m3.ime.unicamp.br/recursos/1051
FRACTALNOW. Programa computacional aberto. Disponível em https://fractalnow.sourceforge.io/