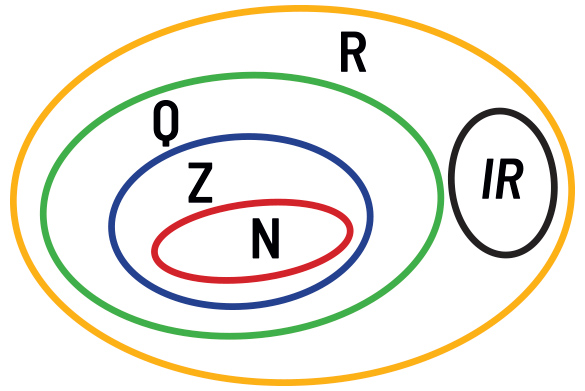
Ao longo da história da humanidade, a ideia de infinito tem provocado espanto e admiração não só entre matemáticos e filósofos, mas também entre as pessoas em geral que refletiram sobre esse conceito ‒ desafiador e aparentemente paradoxal.A própria noção mais elementar de quantidade leva a desdobramentos surpreendentes quando se trata de conjuntos infinitos.Este artigo apresenta uma breve história do infinito e possíveis discussões sobre esse conceito em sala de aula.

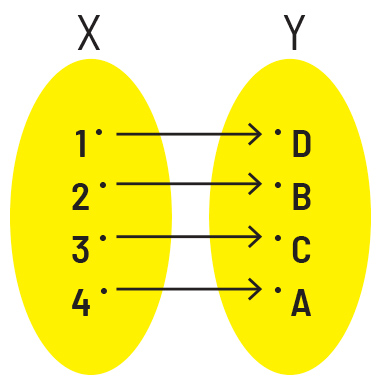
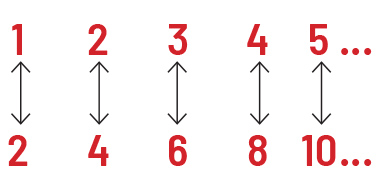
É bastante razoável considerar que dois conjuntos têm a mesma quantidade de elementos se é possível estabelecer entre eles uma correspondência um a um, de forma que não sobrem elementos em nenhum dos dois lados.

A correspondência um a um mostra que existem tantos números naturais quantos números pares.

Crédito: Divulgação

Esse método de correspondência era usado por grupos e povos para controlar quantidades, antes mesmo do advento dos primeiros sistemas numéricos. Por exemplo, segundo fábula comumente narrada em livros de história da matemática, um pastor de ovelhas na pré-história podia controlar a quantidade de seu rebanho fazendo corresponder uma pedrinha a cada cabeça animal. Verdadeira ou não, essa narrativa ilustra a ideia elementar de correspondência um a um, permitindo controlar quantidades sem associá-las a rótulos numéricos.

Aplicando essa mesma ideia (aparentemente simples) a conjuntos infinitos, seria possível concluir, por exemplo, que existem tantos números naturais quanto números pares; ou que há a mesma quantidade de pontos em um segmento de reta de comprimento 1 quanto em um de comprimento 10.

De fato,ao alinharmos todos os números naturais e todos os números pares, podemos construir uma correspondência um a um entre esses dois conjuntos, sem que sobre nenhum número em nenhum dos dois.

Mas como isso é possível?Afinal, como podem dois conjuntos ter a mesma quantidade de elementos se um deles (no caso, o de pares) ‘cabe dentro do outro’ e ainda sobram infinitos elementos?

Essa ideia aparentemente paradoxal corresponde à própria definição matemática de infinito: um conjunto é infinito se é possível retirar dele uma parte e obter uma parte remanescente que continua com a mesma quantidade de elementos que a original. Os matemáticos dizem isso da seguinte maneira:um conjunto é infinito se tem a mesma cardinalidade (quantidade de elementos) que uma parte de si próprio.

Essa ideia extraordinária (no sentido literal da palavra) foi ilustrada pelo matemático alemão David Hilbert (1862-1943), por meio da célebre alegoria conhecida como ‘Hotel de Hilbert’: em um hotel com infinitos quartos, sempre há vagas, mesmo que este esteja lotado.

Vejamos. Suponha que um novo hóspede chegue a esse hotel. Para alojá-lo, o gerente pede que o hóspede do quarto 1 se mude para quarto 2, que este vá para o quarto 3 e assim sucessivamente. Desse modo, o hóspede do quarto ‘n’ se mudará para o quarto ‘n+1’. E o quarto 1 fica liberado para o novo hóspede, sem que ninguém fique desalojado!Note que esse processo é uma correspondência um a um entre os conjuntos {1; 2; 3; …} e {2; 3; 4; …}

O ‘Hotel de Hilbert’, que, apesar de lotado, sempre é capaz de alojar mais um novo hóspede.

Crédito: Divulgação

Paraíso de Cantor

Às vezes, se pensa no infinito como ‘um número muito grande’ ou ‘um número maior que qualquer outro’. Entretanto, as cardinalidades de conjuntos infinitos não podem ser entendidas como números, pois não estão sujeitas às mesmas leis aritméticas que regem estes últimos.

Exercício mental: pense em um número ‘muito grande’. Sugestão: o número 10¹⁰⁰(1 seguido de 100 zeros), batizado como googol, que é muito maior que: i) o número estimado de segundos(6 x 10¹⁸) desde o início do universo (cerca de 13,8 bilhões de anos); ouii) o número estimado de átomos no universo conhecido (6 x10⁷⁹).

Entre os maiores números que já ganharam um nome, está o googolplex: 10^googol (1 seguido de googol zeros).Estima-se que as folhas de papel necessárias para escrever esse número em notação decimal formariam uma pilha cuja altura não caberia no universo observável! No entanto, por maiores que sejam esses números, eles seguem sendo finitos.

Por muito tempo, a ideia de infinito foi vista como algo que não poderia ser considerado um conceito matemático legítimo. O exemplo ilustrado na figura 3 foi apontado pelo físico e matemático italiano Galileu Galilei (1563-1643), em Duas novas ciências (1638), como “paradoxos do infinito”.O matemático alemão Carl Friedrich Gauss (1777-1855) escreveu, em 1831: “Eu protesto contra o uso de uma quantidade infinita como uma entidade matemática verdadeira”.

Só no final do século 19, o conceito de infinito começou a ser aceito como “uma entidade matemática verdadeira”. Isso se deu, em grande parte, por causa dos trabalhos do matemático alemão Georg Cantor (1845-1918). Mas certo ceticismo ainda permaneceu.

Para o francês Henri Poincaré (1854-1912), em seu livro Ciência e método (1908):“É verdade que o cantorismo nos prestou serviços,mas isto era quando o aplicávamos a um verdadeiro problema, cujos termos eram claramente definidos[…].”Hilbert, no entanto, reconheceu de forma incisiva a chamada ‘teoria de Cantor’: “Ninguém nos expulsará do paraíso que Cantor criou para nós.”

Essa breve reflexão histórica pode servir para questionar a concepção – muitas vezes, difundida no ensino básico e superior – de que as ideias e os objetos da matemática “já nasceram perfeitos”. Ou seja, sempre foram e sempre serão como são hoje.

Infinitos maiores que outros

Infinitos são todos iguais? Ou será que alguns são maiores que outros? Até hoje, as respostas para essas perguntas ‒ que, a princípio, soam despropositadas ‒impõem desafios à pesquisa em matemática. Nascem desses questionamentos problemas ainda em solução. Pior: que não podem ser respondidos com base na lógica formal da matemática.

Pode soar estranho, mas, amparado pelo conceito de cardinalidade, pode-se provar que há mais números reais do que naturais – embora ambos sejam infinitos. A demonstração para isso se baseia em um argumento de contradição conhecido como ‘diagonal de Cantor’.

O argumento central é o seguinte: estabelecer uma correspondência um a um entre esses dois conjuntos ‒ como fizemos entre os naturais e os pares. Se tal correspondência fosse possível, poderíamos ligar cada número natural a um número real, obtendo uma ‘lista infinita’.

No entanto, como mostra a figura 4, isso é impossível. E a estratégia para mostrar essa impossibilidade é a seguinte: pegue o 1º algarismo depois da vírgula do número decimal da lista que corresponde ao natural 1; depois, pegue o 2º algarismo depois da vírgula do número decimal que corresponde ao natural 2. E assim por diante.

A ‘diagonal de Cantor’. O novo número criado pelos algarismos selecionados pela faixa amarela difere de cada um dos que aparecem na lista.

Crédito: Divulgação

Com isso, obteríamos um novo número real que diferiria de cada um dos que aparecem nas posições ‒ no caso, 12 delas, mas poderíamos estendê-las indefinidamente ‒ de nossa lista, pois ele tem,certamente,pelo menos um algarismo diferente de todos os decimais listados.Posto em termos simples:em nossa correspondência um a um, ‘sobrariam’ números reais.

Ou seja, o infinito dos reais é maior que o infinito dos naturais. De forma mais geral, a teoria de Cantor estabelece que, para qualquer conjunto infinito dado, é possível tomar outro ainda maior. Isto é, existem na verdade infinitas cardinalidades distintas de conjuntos infinitos.

Racionais versus irracionais

A ideia de infinito está intrinsecamente envolvida em muitos tópicos usualmente estudados na matemática da escola básica. Mas, por vezes, esse conceito é apresentado de forma errada ao aluno. É o caso de alguns diagramas de Venn encontrados em livros didáticos ou na internet que podem levar à ideia (conceitualmente errada) de que o conjunto dos racionais é maior que o dos irracionais ‒ ou mesmo de que existiriam números reais que não são nem racionais, nem irracionais

Diagrama de Venn conceitualmente errado, poisdá a ideia de queo conjunto dos racionais (Q) é maior do que o dos irracionais (I) e de que existem números reais (R) que não são nem racionais, nem irracionais.

Crédito: Divulgação

Além disso, a gama de exemplos usualmente apresentados na escola básica privilegia muito mais os números racionais do que os irracionais. Uma das consequências dessa assimetria é que, em geral, os alunos conseguem citar muitas frações, mas pouquíssimos números irracionais‒ talvez, os mais conhecidos sejamπ, √2 e √3.

Antes de prosseguirmos, uma breve revisão: racionais são todos os números que podem ser escritos na forma de a/b, com b ≠ 0 (o que inclui os naturais {0, 1, 2, 3…} e os inteiros {…-2, -1 0 1, 2…}); os irracionais são aqueles que não podem ser representados assim, como o π (3,1415…) e a √2 (1,4142…). Isto é, os irracionais são os números reais que não são racionais.

A maior crítica a essas escolhas de representações e exemplos para números racionais e irracionais na escola básica não é a possibilidade de levarem a ideias matematicamente erradas, mas, sim, a de construção implícita de um sentido de ‘normalidade’, associado ao que é ‘regular’ ou ‘bem comportado’.

Os números irracionais são tratados como ‘exceções’ ou ‘casos patológicos’ – quando, na verdade, no sentido das cardinalidades, são a maioria dos números reais. Não é o caso de demonstrar esse fato aqui ‒ e se pode questionar que essa demonstração tampouco seja adequada para a escola básica. Mas há alternativas mais intuitivas: pedir ao aluno que construa um número escolhendo aleatoriamente (por sorteio, por exemplo), um a um,os algarismos de sua representação decimal.

Desse modo, seria altíssima a probabilidade de o número criado ser não periódico‒ e, portanto, ser irracional. Essa estratégia indica que o ‘irregular’ é muito mais provável que o ‘regular’. Mais: surge aí a chance de discutir que, em matemática, o ‘regular’ é que é exceção.

Em discussões como essas, o importante ‒ por contribuir para a construção do conhecimento pelos alunos ‒ é justamente a provocação causada por ideias surpreendentes ou aparentemente contraditórias. Infelizmente, estratégias pedagógicas assim são quase sempre tratadas superficialmente ou sistematicamente evitadas.

‘Verdades absolutas’

O ensino de matemática na escola básica (e também na universidade) está mais pautado pela apresentação de resultados e fatos estabelecidos do que por uma abordagem problematizada em que se destaque o modo como as ideias matemáticas são produzidas, bem como os sentidos atribuídos histórica e socialmente a elas.

Parece haver uma concepção equivocada de que qualquer forma de abordagem que escape à simples apresentação de fatos e resultados corresponda a um ‘enfraquecimento do conteúdo matemático’ – quando, na verdade, é justamente o contrário: a problematização de ideias pode aprofundar o conteúdo.

Uma limitação do ensino de matemática e ciências pautado pela exposição de resultados e fatos prontos é que as ideias científicas tornam-se‘verdades absolutas’ e, assim, acabam fazendo tanto sentido quanto qualquer outra coisa. Isso acaba igualando teorias e modelos baseados em dados empíricos e comprovados experimentalmente (por exemplo, darwinismo e estrutura planetária) a conjecturas pseudocientíficas, como o‘criacionismo’ e a ‘terra plana’ ‒ afinal, todas essas ideias parecem igualmente ‘verdades absolutas’.

A solução para isso é fazer com que os estudantes produzam sentido para os conhecimentos matemático e científico. E isso é obtido quando esse conhecimento é discutido na escola de forma problematizadora, isto é, a partir de seus processos de produção ‒ e não simplesmente como verdades estabelecidas.

O conceito de infinito ‒ por envolver ideias surpreendentes e aparentemente paradoxais ‒é terreno fértil para discussões pela perspectiva da produção de conhecimento matemático, levando o aluno a produzir um sentido para o conteúdo a ele oferecido.

Há uma concepção comum – e que, recentemente, tem ganhado força – de que o ensino de matemática pode ser ‘apolítico’ ou ‘despolitizado’ ‒ talvez isso ocorra pelo fato de a matemática ser vista como ‘ciência exata’. Porém, as escolhas feitas na escola determinam que sentidos serão produzidos para o conhecimento e que lugar esses sentidos terão na vida dos aprendizes. Portanto, educação é sempre política, e a tentativa de despolitizá-la é, em si, uma política.