Um joguinho popular – cujo desafio é encontrar rapidamente figuras em comum entre duas cartas – está baseado em conceitos ‘ocultos’ de uma área da matemática: a geometria projetiva finita, que lida basicamente com pontos e linhas que se cruzam

Um joguinho popular – cujo desafio é encontrar rapidamente figuras em comum entre duas cartas – está baseado em conceitos ‘ocultos’ de uma área da matemática: a geometria projetiva finita, que lida basicamente com pontos e linhas que se cruzam

A geometria é o ramo da matemática que trata das propriedades do espaço (distâncias, formas e áreas). Até o século 19, falar em geometria era falar em geometria euclidiana – referência a Euclides (3 a.C.), que sistematizou o conhecimento da área até aquele momento.
Esse matemático grego fez isso com base em axiomas – proposições consideradas autoevidentes – e regras de dedução lógica. Exemplos: “por dois pontos, passa uma única reta” (axioma) e “se A é igual a B, e B igual a C; então, A é igual a C” (dedução lógica).
A partir do fim do século 19, surgiram outras geometrias. Por exemplo, a projetiva, como desdobramento da técnica da perspectiva usada por artistas.
A geometria projetiva trata de pontos e linhas – qual ponto está em qual linha; quais linhas se cruzam –, como na perspectiva, e não de distâncias e ângulos. Ambas têm conceitos semelhantes, como os ‘pontos no infinito’ (geometria projetiva) e ‘pontos de fuga’ (arte) – estes últimos podem ser observados, por exemplo, nas margens de uma longa estrada reta.
Os ‘pontos de fuga’ lembram um conceito da geometria euclidiana, o das retas paralelas, as quais nunca se cruzam. Na geometria projetiva, porém, não existem retas paralelas, pois todas se cruzam.
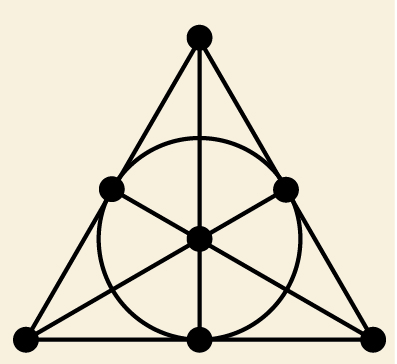
A geometria projetiva tem uma subárea: a geometria projetiva finita, que lida com um número finito de pontos e linhas. Exemplo dela está na figura a seguir: o ‘plano de Fano’, homenagem ao matemático italiano Gino Fano (1871-1952). Nela, temos sete pontos e sete linhas – no caso, os lados e as alturas do triângulo, bem como o círculo.
Para acessar este ou outros conteúdos exclusivos por favor faça Login ou Assine a Ciência Hoje.

Um dos principais nomes da IA generativa, o cientista da computação Hao Li vislumbra um futuro em que a tecnologia será capaz de criar humanos digitais, reconstituir o passado e construir metrópoles em tempo real. Mas ele reconhece dilemas éticos: ‘O importante é as pessoas saberem o que é possível’

Cientistas de diversas áreas do conhecimento e diferentes nacionalidades desenvolveram um algoritmo capaz de identificar as barragens que poderiam gerar eletricidade de forma mais vantajosa, causando o menor dano possível na região
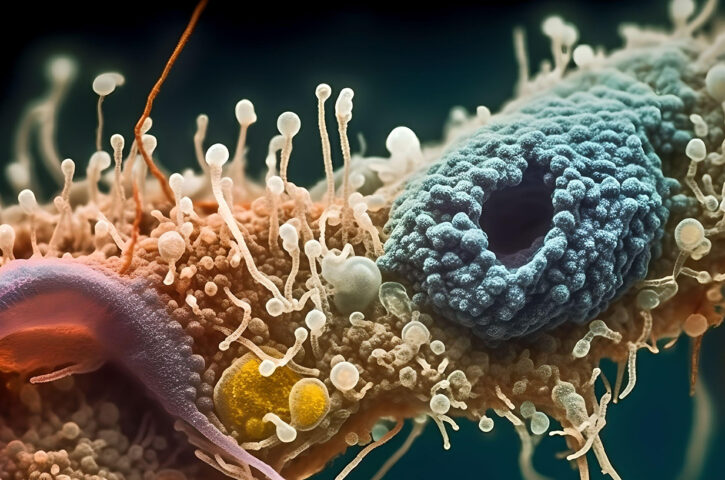
“Aquilo que sabemos é pouco; o que não sabemos é imenso”. A frase atribuída ao cientista francês Pierre-Simon Laplace (1749-1827) cai sob medida para o quanto ainda desconhecemos sobre a diversidade dos protozoários, diminutos seres onipresentes na natureza

Por que insetos caminham sobre a água? Por que se forma o orvalho? A explicação para esses fenômenos começou ainda na Antiguidade. Hoje, a ciência das interações intermoleculares tem aplicações na medicina e na indústria – e no cotidiano

A macroecologia é uma área multidisciplinar que estuda padrões de biodiversidade em grande escala. Essa disciplina inovadora tem também ajudado nos estudos sobre mudanças climáticas, como ferramenta para a elaboração de políticas de sustentabilidade.

Entender a natureza dos fatores envolvidos na origem desse transtorno mental pode ajudar na busca por novas formas de tratamento. Evidências mostram que intervenções sobre o sistema imune podem beneficiar alguns pacientes com essa condição psiquiátrica

O uso de mecanismos genômicos no tratamento das doenças de Alzheimer ou Parkinson pode produzir perspectivas terapêuticas importantes. Estudos recentes mostram que uma versão de um determinado gene pode conferir proteção contra essas enfermidades.
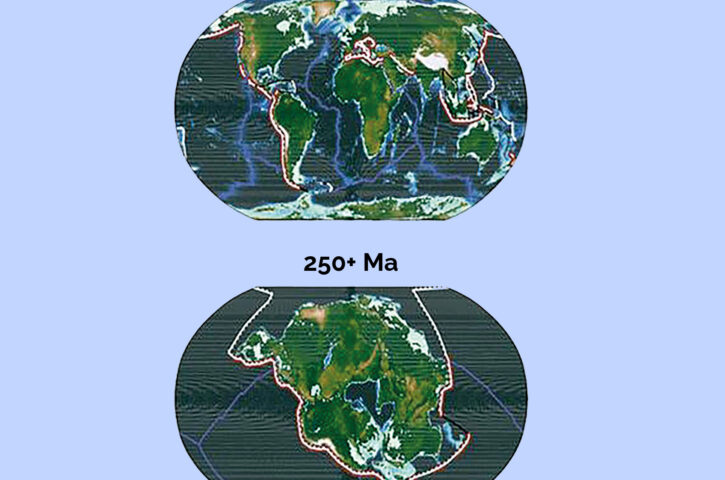
Pesquisadores projetam que a formação de uma extensa massa continental, denominada Pangeia Última, daqui a cerca de 250 milhões de anos, vai gerar condições climáticas extremas, sobretudo um aquecimento global que irá restringir as regiões habitáveis do planeta

Os prêmios Nobel de Física e Química deste ano contemplaram trabalhos que investigaram a matéria em sua mais diminuta escala: a atômica e subatômica. E esses resultados têm aplicações práticas que vão da área eletrônica até o tratamento do câncer

Noel e seu ajudante irritante e sonolento, Günther, voltaram. Este ano, fui eu que apresentei um desafio: uma ‘mágica’ com cartas de baralho. A dupla fez um lanchinho, mas, antes que eu pudesse mostrar a solução do problema, eles partiram, deixando um ‘recadinho’

O ‘amigo húngaro’ desta coluna retorna. Mais uma vez, com um desafio extraído de sua lista de problemas favoritos, conhecidos por exigir somente uma ‘bagagem’ matemática básica, mas cuja resolução pode ser desafiadora. Mas a intuição está aí para nos dar uma mãozinha

Quer se transformar num mágico? A matemática pode te dar uma ajuda valiosa. Para executar o truque, você precisará de uma ‘vítima’ e um baralho com 52 cartas. Ao final do espetáculo, você, certamente, vai deixar a audiência encantada com seus ‘poderes’ mentais

“Pensei em um número de 1 a 100. Qual é o número?” Provavelmente, você conhece ou já participou de jogo assim. Mas qual o número mínimo de perguntas que você terá que fazer a seu oponente para descobrir o número pensado por ele? A resposta é pura matemática

É possível saber se uma informação é verdadeira sem que nada seja revelado sobre ela? Dois amigos, uma caverna, uma palavra ‘mágica’ e um espião – somando-se a isso boa dose de ciência da computação e criptografia – mostram como responder a essa intrigante questão

Neste mês, mais curiosidades de um jogo de tabuleiro para dois competidores, estimulante e simples de jogar, e no qual nunca há empates. Nele, portanto, um dos adversários deve ter necessariamente vantagem sobre o outro. Mas qual deles: o primeiro ou o segundo a jogar? E por quê?

Natal. E Noel veio... de novo – claro, com Günther, o comilão. Mais uma vez, nada de presentes do ‘bom velhinho’, mas ele, como sempre, deixou um desafio interessante escrito em um papelzinho: uma sequência de letras que devem formar pares entre si

A matemática pode ser uma ferramenta útil também no mercado editorial. Nesta coluna, veremos como a teoria das probabilidades pode nos ajudar a quantificar as chances de dois revisores de uma editora, trabalhando de forma independente, encontrarem erros de digitação nas provas de um livro
| Cookie | Duração | Descrição |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
