Sabe aquele colchão novo, ultramoderno, que você comprou para ter noites confortáveis de sono? Bem, com o tempo, ele certamente vai causar incômodo. A boa notícia é que a solução do problema é fácil. E ainda vai ensinar um pouco de matemática
Sabe aquele colchão novo, ultramoderno, que você comprou para ter noites confortáveis de sono? Bem, com o tempo, ele certamente vai causar incômodo. A boa notícia é que a solução do problema é fácil. E ainda vai ensinar um pouco de matemática
CRÉDITO: FOTO ADOBE STOCK
Imagine que você comprou um colchão novo, ultramoderno. O fabricante garante sono tranquilo e até ‘sonhos dourados’. No início, isso é assim. Mas…
Com o tempo, surgem incômodos, aqui e ali. Ao ler o folheto que veio com o colchão, você nota a seguinte instrução: “Realizar giro mensalmente”.
Giro? O que é isso? Com um pouco mais de pesquisa, você descobre: com o tempo, o colchão se deforma com o peso do corpo. Para resolver isso, o fabricante sugere que se gire o colchão periodicamente.
Começa aqui nossa investigação matemática: o estudo da teoria de grupos.
Para facilitar as coisas, vamos imaginar que nosso colchão é quadrado e recoberto com tecido liso e de uma só cor. Então, quando o girarmos, não notaremos diferença entre a nova posição e a antiga.
No fundo, queremos estudar as ‘simetrias do quadrado’. O físico estadunidense Richard Feynman (1918-1988) deu uma explicação intuitiva desse conceito: “Uma coisa é simétrica se depois de sujeitá-la a uma operação ela parece a mesma coisa”.
Vamos desenhar nosso colchão e marcar nele pontos especiais com letras. Na figura, A, B, C e D são os vértices; P, Q, M e N, os pontos médios dos lados.
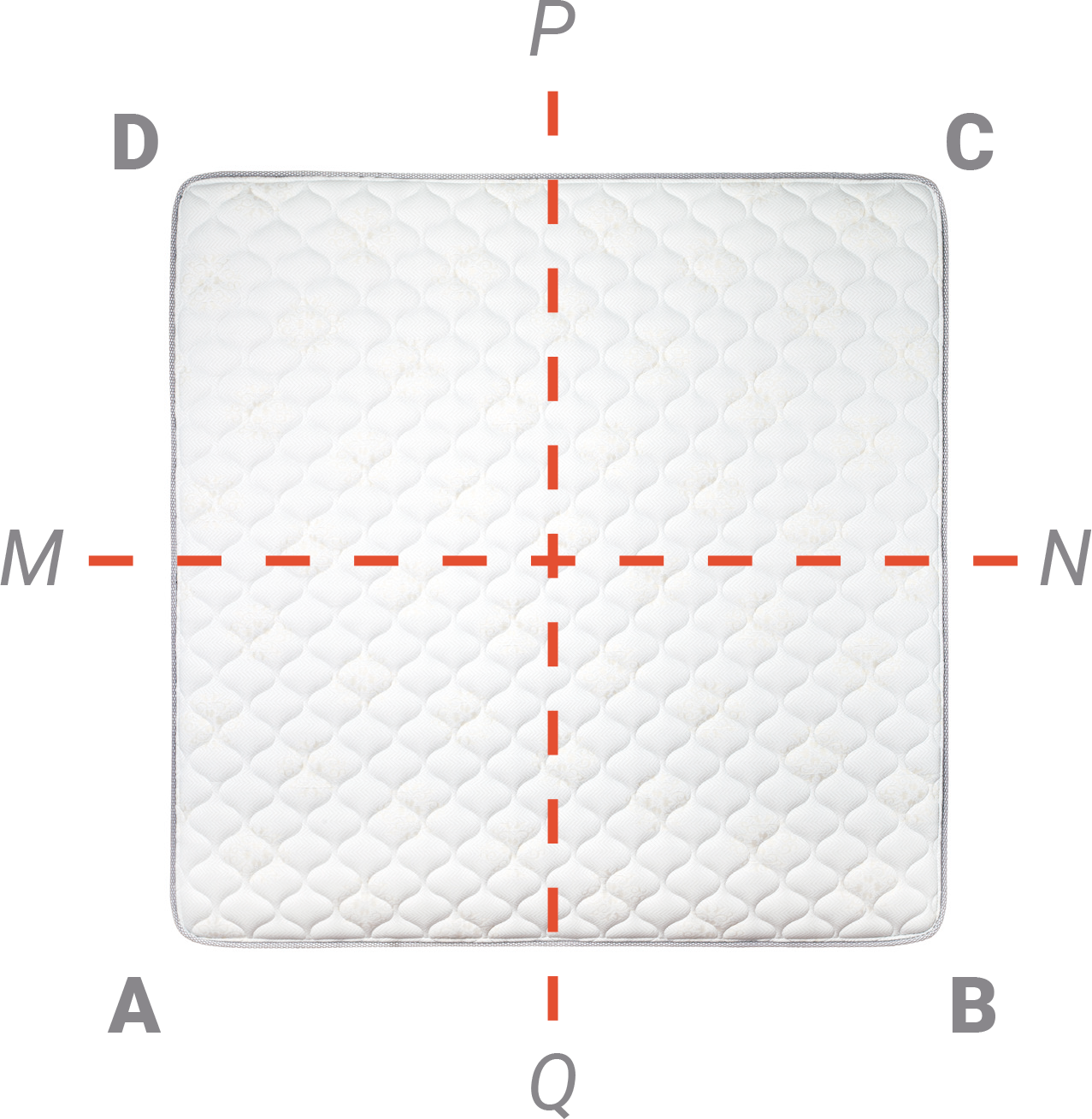
A primeira operação de simetria que podemos fazer no colchão é… não fazer nada. Soa estranho, mas, matematicamente, faz sentido. Tecnicamente, ela é denominada ‘operação identidade’ (I).
Podemos também girar o colchão 90o no sentido horário. Ou 180o, ou 270o, ou 360o. Ou fazer isso no sentido anti-horário.
A rotação mais simples (90o) é chamada R. A de 180o (duas rotações R) é denominada R2. Portanto, a de 270o será R3; e a de 360o, R4 – note que esta última é igual a ‘não fazer nada’. Então, R4 = I.
Ainda há outras operações que podemos realizar: reflexões por eixos que passam pelos pontos médios dos lados opostos.
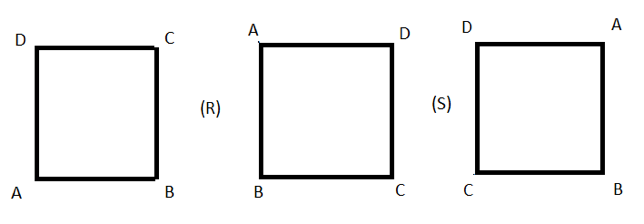
Se ‘refletirmos’ o quadrado pelo eixo PQ, trocaremos as posições de A e B, bem como as de C e D. Chamaremos essa operação de S. Se fizermos o mesmo com o eixo MN, trocaremos as posições de A e D, e as de B e C. Essa será a operação S’ (S linha).
Essa operação não é independente das outras, pois S’ = RRS = R2S. Faça o desenho para ver o porquê! Note que as operações são feitas da direita para a esquerda: primeiro S; depois, R; depois, R, novamente.
Podemos refletir o quadrado pelas diagonais: i) trocando A com C e mantendo B e D ‘parados’ (operação T); ou ii) trocando B com D e mantendo A e C ‘parados’ (operação T’). Essas operações podem ser escritas assim: T = SR e T’ = RS. Na verdade, podemos também expressar T = R3S (mais um desenho!).
Finalmente, esgotamos as simetrias do quadrado. A lista completa é: I, R, R2, R3, S, RS, R2S, R3S.
Por que elas se esgotam? Porque, no caso do quadrado, não há operação que mude a distância entre vértices. Por exemplo, não é possível fazer com que A e B sejam diagonalmente opostos.
O quadrado nos dá uma introdução à teoria de grupos, estudo das simetrias de objetos matemáticos (triângulos, círculos, esferas, poliedros e até figuras geométricas mais abstratas).
Por que simetrias do quadrado nesta coluna? Ora, o tempo todo eu estava com um quadrado muito especial na cabeça: 202, ou seja, 400. Parabéns à Ciência Hoje por sua quadringentésima edição. Que venha muito mais dessa revista fabulosa. E que possamos dormir tranquilos – sempre lembrando de girar o colchão.
Explique por que T = SR.
Visualmente, aplicando R (rotação de 90º) e, depois, S (reflexão pelo eixo P e Q), veremos que isso equivale a uma reflexão T (reflexão pela diagonal BD do quadrado original). De modo semelhante, se mostra que T = R3S.
Para Daniel Cara, professor e pesquisador da USP, reforma é descontextualizada do universo escolar e das realidades das redes públicas, busca ‘desprofissionalizar’ docentes, impõe uma educação desprovida de ciência e não proporciona o direito de escolha aos estudantes, alardeado pelos defensores do NEM
A partir de mergulhos e com a ajuda de tecnologias de levantamento geofísico, pesquisadores acharam restos de embarcações naufragadas na região do Bracuí (RJ) que poderiam ser do brigue norte-americano Camargo, um dos últimos a trazer ilegalmente africanos para o país
A escassez de água potável já afeta cerca de 0,5 bilhão de pessoas no planeta. E essa crise deve aumentar nas próximas décadas, por causa das mudanças climáticas, do crescimento populacional e aumento da poluição. Novos materiais porosos prometem uma solução peculiar: extrair água do ar
Geneticista norte-americana decifrou, no início do século 20, a incógnita sobre como é definido o sexo biológico na reprodução, mas não teve seu trabalho devidamente reconhecido em vida por ser mulher em uma comunidade científica dominada por homens
Nesta data especial em que a Ciência Hoje chega à edição n⁰ 400, Alexander Kellner apresenta um breve histórico da criação da coluna Caçadores de fósseis, a mais antiga em atividade na revista, com 184 textos publicados até hoje, alguns reunidos em um livro
Estranhamente, a natureza parece ter predileção por simetrias de formas e cores. E, de certo modo, isso pode ser denominado beleza, noção que tem guiado a pesquisa científica no entendimento dos fenômenos que vão da escala subatômica ao gigantismo do cosmos
Um jogo simples em que cada participante deve escolher um número dentro de certo intervalo tem uma resposta lógica (e surpreendente) se os jogadores forem matemáticos. Mas, no mundo real, a coisa é mais bem complicada, como mostram os economistas
Quatro copos sobre uma mesa giratória. Problema: deixá-los todos virados para cima ou para baixo. Trivial? Sim. Mas, agora, faça isso com os olhos vendados, e esse desafio se torna um jogo muito interessante do ponto de vista lógico. Difícil? Não se preocupe: a matemática, mais uma vez, vai te ajudar.
Máximus, o mágico, está de volta. E vem com um truque que, como sempre, deixará Vítor, seu assistente-vítima, surpreso e espantado. Desta vez, o mestre das ilusões nos apresenta uma tabela com propriedades intrigantes. Seja bem-vindo, bem-vinda, a mais um show de ‘matemágica’!
Teoria da probabilidade causa ‘derrapadas’ até mesmo em matemáticos experientes, pois a aleatoriedade pode dar um ‘nó’ em nossos cérebros. Mesmo problemas aparentemente simples podem levar a resultados distintos: é preciso saber não só ‘o que’ se calcula, mas ‘como’ se faz isso
O velhinho de barbas longas e seu insuportável ajudantezinho deram as caras de novo. E, desta vez, com uma oferta irrecusável: pedaços de barra de chocolate. Será que Noel é um ser redimido e, este ano, vai finalmente ser generoso comigo, sem truques, surpresas (desagradáveis), enganação? Ou...?
Um tutor se diverte com seu vira-lata em um parque, ambos dando voltas em torno de uma árvore. Nessa cena corriqueira do cotidiano, está embutido um teorema de consequências profundas e importantes para a matemática. Mais: ele pode ser entendido só com palavras, sem qualquer cálculo.
Por que sempre é possível apoiar um poliedro convexo em uma de suas faces sobre uma mesa de modo que ele não tombe? E por que ele tomba se apoiado sobre um de seus vértices? Haveria um poliedro que tombasse indefinidamente? Será que a intuição da física pode nos ajudar a resolver esse problema geométrico?
Um professor desafia três ex-alunas com um problema matemático envolvendo placas com trincas de números. Usando a lógica como principal ferramenta, elas desvendam o enigma e mostram como toda informação é importante para construir uma sequência de deduções e chegar a conclusões perfeitas
Três sapos e três rãs se encontram alinhados em um ‘tabuleiro’ de uma só linha com sete casas. Para se movimentar, eles podem deslizar para um mesmo lado ou pular um por cima do outro. Será possível trocar os grupos de anfíbios de lugar, invertendo as posições?
