Curioso objeto bidimensional com apenas um lado foi descrito por dois cientistas pupilos do ‘príncipe da matemática’ no século 19 e inspira até esteiras de bagagens de aeroportos e escadas rolantes
Curioso objeto bidimensional com apenas um lado foi descrito por dois cientistas pupilos do ‘príncipe da matemática’ no século 19 e inspira até esteiras de bagagens de aeroportos e escadas rolantes
crédito: a partir de wikimedia

Consegue imaginar uma superfície bidimensional com apenas um lado? Esse estranho objeto que desafia o senso comum existe e é a fita de Möbius. Pode parecer absurdo, mas, se uma formiga caminhasse ao longo dessa fita, percorreria tanto a parte interna quanto a externa sem precisar saltar de um lado para outro. Não acredita? Siga o passo a passo para montar a fita de Möbius, passe o dedo pela superfície dela e vai perceber que seu dedo vai voltar ao lugar de partida sem que seja preciso levantá-lo da fita.
Esse objeto surpreendente foi descrito, de forma independente, porém no mesmo ano de 1858, por dois matemáticos alemães, August Ferdinand Möbius (1790 – 1868) e Johann Benedict Listing (1808 – 1882). De fato, Listing descreveu a fita alguns meses antes de Möbius, mas sua pesquisa foi publicada apenas em 1861. Além disso, Möbius era um cientista de maior prestígio naquela época, e seu nome prevaleceu na história.
Esse objeto surpreendente foi descrito, de forma independente, porém no mesmo ano de 1858, por dois matemáticos alemães
Möbius e Listing foram pioneiros do campo da topologia, uma disciplina que estuda as propriedades dos objetos geométricos e suas características frente a forças que causam deformações, ou seja, como esses objetos podem ser torcidos, esticados, amassados e dobrados. O grande matemático Leonhard Euler (1707 – 1783) foi o fundador da topologia, mas o estudo da fita de Möbius e suas curiosas características promoveu grandes avanços nessa área. As fitas de Möbius recebem uma classificação exclusiva na topologia, elas são objetos não-orientáveis. Explicando de forma simples, isso quer dizer que se desenharmos uma seta sobre ela, não podemos concluir se a seta está apontando para cima ou para baixo.
As fitas de Möbius recebem uma classificação exclusiva na topologia, elas são objetos não-orientáveis
Descendente de Lutero
Möbius era filho de um professor de dança, que faleceu quando o menino tinha apenas 3 anos. Sua mãe era descendente direta de Martinho Lutero (1483-1546) e educou o futuro matemático em casa até os 13 anos. A partir daí, Möbius começou a frequentar a escola no famoso monastério de Pforta, na Saxônia. Desde cedo, demonstrou afinidade pela matemática, mas, como sua família o pressionava para que seguisse uma carreira no Direito, ele iniciou seus estudos nessa área na prestigiosa Universidade de Leipzig. Foi lá que conheceu o matemático e astrônomo Karl Mollweide (1774-1825), e não teve dúvidas: trocou seu curso de estudos para astronomia e matemática. Mollweide era um cientista brilhante e foi grande influência na carreira de Möbius. Após se formar, ainda teve a fortuna de trabalhar na Universidade de Göttingen com ninguém menos que Carl Friedrich Gauss (1777-1855), o “Príncipe da Matemática”.
A carreira acadêmica de Möbius teve altos e baixos, em grande parte devido a sua timidez. Apesar de receber ofertas de instituições menos prestigiosas, ele almejava uma posição de professor titular na Universidade de Leipzig, mas as coisas não aconteceram como planejava. Ele não era visto como um orador talentoso, e suas palestras e cursos não atraíam muitos alunos (que pagavam as taxas e mensalidades da universidade). Apesar de trabalhar na Universidade de Leipzig desde 1816, ele foi nomeado professor titular apenas em 1844. Möbius também era astrônomo do Observatório de Leipzig, onde fez inúmeras contribuições para a astronomia, particularmente no ramo que estuda os movimentos dos corpos celestes. Por isso, o cientista tem seu nome associado a diversas contribuições na matemática, como a Fórmula de Inversão de Möbius e a Função de Möbius, mas sua mais famosa descoberta, a fita de Möbius foi feita enquanto ele trabalhava em um outro desafio proposto pela “Académie des Sciences” da França: sobre a teoria geométrica dos poliedros, que são figuras sólidas compostas de vértices, arestas e faces planas.
Apesar de ser um matemático brilhante, a coincidência acerca da descoberta da fita ter sido feita por Möbius e Listing com apenas alguns meses de diferença pode não ter sido fruto do acaso. Os dois cientistas haviam sido alunos de Gauss, que por sua vez tinha o hábito de não publicar ou desenvolver todas as suas ideias. Em relação aos seus resultados, seu lema era Pauca sed matura (Poucos, mas maduros), ou seja, ele só publicava quando estava inteiramente satisfeito. Assim, uma grande parte dos seus trabalhos só foi descoberta após a sua morte. Muitos autores e historiadores atuais acreditam que a ideia original da fita veio de Gauss, e os dois cientistas desenvolveram o conceito.
Hoje em dia as aplicações da fita de Möbius vão muito além do que Möbius e Listing poderiam ter imaginado. Esse conceito pode ser usado em esteiras de aeroportos e escadas rolantes de shoppings, para garantir que o desgaste aconteça de maneira uniforme e aumente a vida útil do equipamento; em fitas magnéticas que permitem a gravação e reprodução contínua de áudio; fitas de impressora ou de máquinas de datilografar; em resistores que não geram interferência magnética; na pesquisa de supercondutores; em estruturas de grafeno para componentes de nanoeletrônica, etc. A topologia também já esteve presente em pesquisas agraciadas com o prêmio Nobel, sendo o mais recente o Nobel da Física em 2016, que descreveu novos estados da matéria, com implicações importantes para o desenvolvimento de supercondutores e superfluidos.
Além das aplicações tecnológicas, essa estranha fita tem servido de inspiração para artistas, como o artista gráfico holandês M.C. Escher (1898-1972), com suas obras que desafiam nossa percepção. E para casais apaixonados, que veem a fita de Möbius como um símbolo do amor eterno, um caminho sem fim, que aparenta ter dois lados, mas só tem um.
Pegue uma folha de papel e uma tesoura. Em seguida, corte uma fita de cerca de 20 cm de comprimento x 3 cm de largura. Com uma caneta, marque o canto superior esquerdo da fita com a letra A; faça o mesmo no canto inferior esquerdo, assinalando com a letra C. Do outro lado da fita, coloque a letra B no canto superior direito e D no canto inferior direito. Faça então um meio-giro (180º) na fita ao longo do seu eixo e junte as duas pontas formando um objeto circular: letra A sobre a letra D; letra B sobre a letra C. Para terminar, una as duas pontas com uma fita adesiva. Pronto, você tem em mãos uma fita de Möbius!

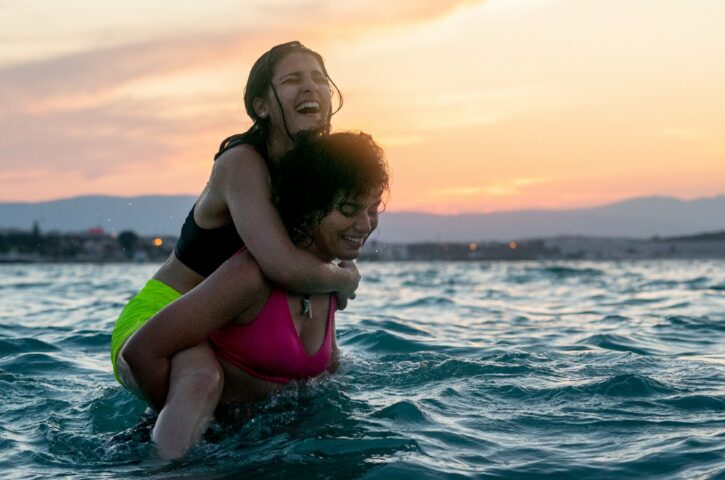
Retratando a vida de duas jovens sírias obrigadas a fugir de seu país, o filme As nadadoras, disponível na Netflix, desponta como enunciador político das tramas do refúgio ao exibir tanto os efeitos da guerra quanto os de um regime de fronteiras cada vez mais hostil
Registros biológicos evolutivos permitem comprovar que todos os seres vivos da Terra derivam de um único ser vivo primordial, um ancestral comum universal que teria surgido há cerca de 4 bilhões de anos, resultando na diversificação e seleção de espécies.
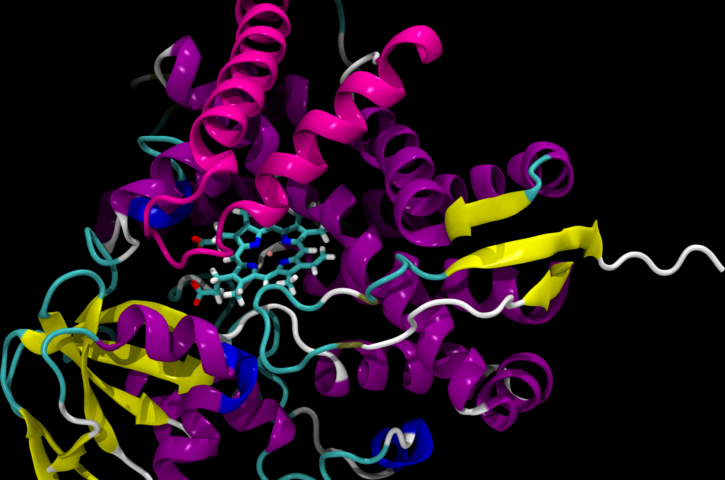
A técnica de simulações moleculares, aliada à extrema capacidade de supercomputadores, é capaz de, partindo de ‘fotos’ dos átomos obtidas por raios X, fazer ‘filmes’ sobre o movimento desses constituintes da matéria. As aplicações desse poderoso método vão da gasolina renovável à infeção pelo coronavírus.

Quando pensamos em bactérias, logo nos vem à cabeça uma palavra: doença. Mas esses microrganismos podem ter papel importante para a indústria e o meio ambiente. Exemplo disso são as bactérias que ajudam a tratar um grande problema ambiental da atualidade: resíduos da mineração.

Longe de estar ultrapassado, o avanço fraudulento sobre terras alheias ou públicas, tão comum na época colonial, se mantém até hoje como uma prática constitutiva do espaço agrário, sendo o próprio Estado o responsável pela regularização e pelo amparo da dinâmica em curso.

Exames mostram que animal de um grupo caracterizado pela presença de ossos pontiagudos em torno do pescoço e nos ombros não era muito ativo e vivia de modo mais solitário, com poucas interações com outros membros de sua espécie

Tente imaginar o mundo sem a eletricidade. Impossível. Razão: ela é provavelmente o insumo mais importante da sociedade. A ciência a domou e a fez trabalhar em prol da humanidade. Um dos grandes desafios hoje é produzi-la sem poluir (ainda mais) o planeta

No final da Segunda Guerra Mundial, dez cientistas alemães foram encarcerados em uma casa na Inglaterra, onde todos os aposentos estavam equipados com microfones ocultos, permitindo que as forças aliadas escutassem as conversas entre mentes brilhantes

A história do uso da impressão digital para reconhecimento de pessoas tem início sombrio: o assassinato de duas crianças. Pioneiro no campo da criminologia, o croata naturalizado argentino Juan Vucetich usou a papiloscopia pela primeira vez em 1892 para desvendar o verdadeiro autor do crime.

As descobertas do bioquímico brasileiro Leopoldo De Meis tiveram um papel fundamental na compreensão do mecanismo de funcionamento da enzima ATP-sintase para sintetizar o ATP, a molécula-chave nas conversões de energia nas células dos seres vivos.

Pioneira da física no Brasil, ela deu contribuições importantes para o entendimento dos raios cósmicos, núcleos atômicos de alta energia que chegam do espaço e bombardeiam a atmosfera terrestre a todo instante, criando uma ‘chuveirada’ de novas partículas que penetram nossos corpos

Data de 1912 a primeira tentativa de se criar um método para medir a ardência das pimentas, e o feito coube a um promissor farmacêutico, que iniciou na carreira fazendo entregas, lavando chão e limpando vitrines.
| Cookie | Duração | Descrição |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
