Pegue a soma dos inversos dos números pares: 1/2 + 1/4 + 1/6 +…. Será que ela diverge?
A adição é uma das primeiras operações matemáticas que aprendemos. Adicionar dois números acaba se tornando tão natural que, para dizermos que algo é muito evidente, usamos a expressão “tão certo quanto 2 + 2 = 4”. Mas e se continuarmos somando números, uma infinidade deles, será que a tal obviedade se mantém?
À primeira vista, poderíamos imaginar que somar números incessantemente resultará em um número cada vez maior. Um exemplo simples é 1 + 2 + 3 + … .
Marco Moriconi
Instituto de Física,
Universidade Federal Fluminense
Para acessar este ou outros conteúdos exclusivos por favor faça Login ou Assine a Ciência Hoje.
O embate entre ciência e religião ocorre, pelo menos, desde o século 15. Desde lá, a ciência vem avançando e desvendando muitos aspectos sobre o mundo físico, enquanto a religião tem se ocupado de teses que pretendem questionar a noção de que a vida na Terra se formou por leis naturais. Uma delas é o design inteligente, que atualmente busca se estabelecer como grupo de pesquisa dentro de universidades.
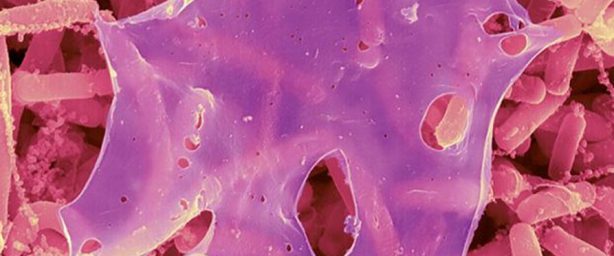
Robôs controlados magneticamente são capazes de exterminar os biofilmes, que são colônias de bactérias com efeitos devastadores não só para o corpo humano (infecções e outras complicações), mas também para a indústria, setor em que geram prejuízos anuais na casa dos bilhões de dólares.
Neste mês, mais curiosidades de um jogo de tabuleiro para dois competidores, estimulante e simples de jogar, e no qual nunca há empates. Nele, portanto, um dos adversários deve ter necessariamente vantagem sobre o outro. Mas qual deles: o primeiro ou o segundo a jogar? E por quê?
Natal. E Noel veio... de novo – claro, com Günther, o comilão. Mais uma vez, nada de presentes do ‘bom velhinho’, mas ele, como sempre, deixou um desafio interessante escrito em um papelzinho: uma sequência de letras que devem formar pares entre si
A matemática pode ser uma ferramenta útil também no mercado editorial. Nesta coluna, veremos como a teoria das probabilidades pode nos ajudar a quantificar as chances de dois revisores de uma editora, trabalhando de forma independente, encontrarem erros de digitação nas provas de um livro
Com só uma regra simples, denominada ‘condição de neutralidade’, um joguinho fácil, divertido e instrutivo – para o qual você só precisa de uma folha de papel e quatro canetinhas de cores diferentes – vai te revelar uma surpreendente propriedade sobre tabuleiros coloridos
Um problema que pode ser simulado com elásticos e preguinhos sobre uma tábua de madeira não é só interessante, instrutivo e divertido, mas também tem papel de destaque na história da matemática, pois sua resolução tem algo dos roteiros de filmes românticos
Duas irmãs e duas amigas delas. Todas as quatro excelentes tenistas. Elas decidem disputar, entre elas, um torneio do tipo ‘perdeu, tá fora’. Qual a probabilidade de as duas irmãs se enfrentarem? Soa complicado. Mas a matemática está aí para simplificar as coisas
Uma intoxicação atinge amigos em um acampamento. No hospital, o médico de plantão enfrenta problema sério: como dar a cada paciente o maior número possível de doses de uma vacina (sem exceder o limite seguro), quando os três tipos de imunizante vieram sem rótulos?
Claro, Noel e seu ‘simpático’ ajudante, Gunther, apareceram. Desta vez, abriram presentes, comeram bolo e usaram – para variar – um truque ‘desleal’: apresentaram ao dono da casa um problema fácil para, depois, complicar as coisas. Mas, no fim, foi divertido
