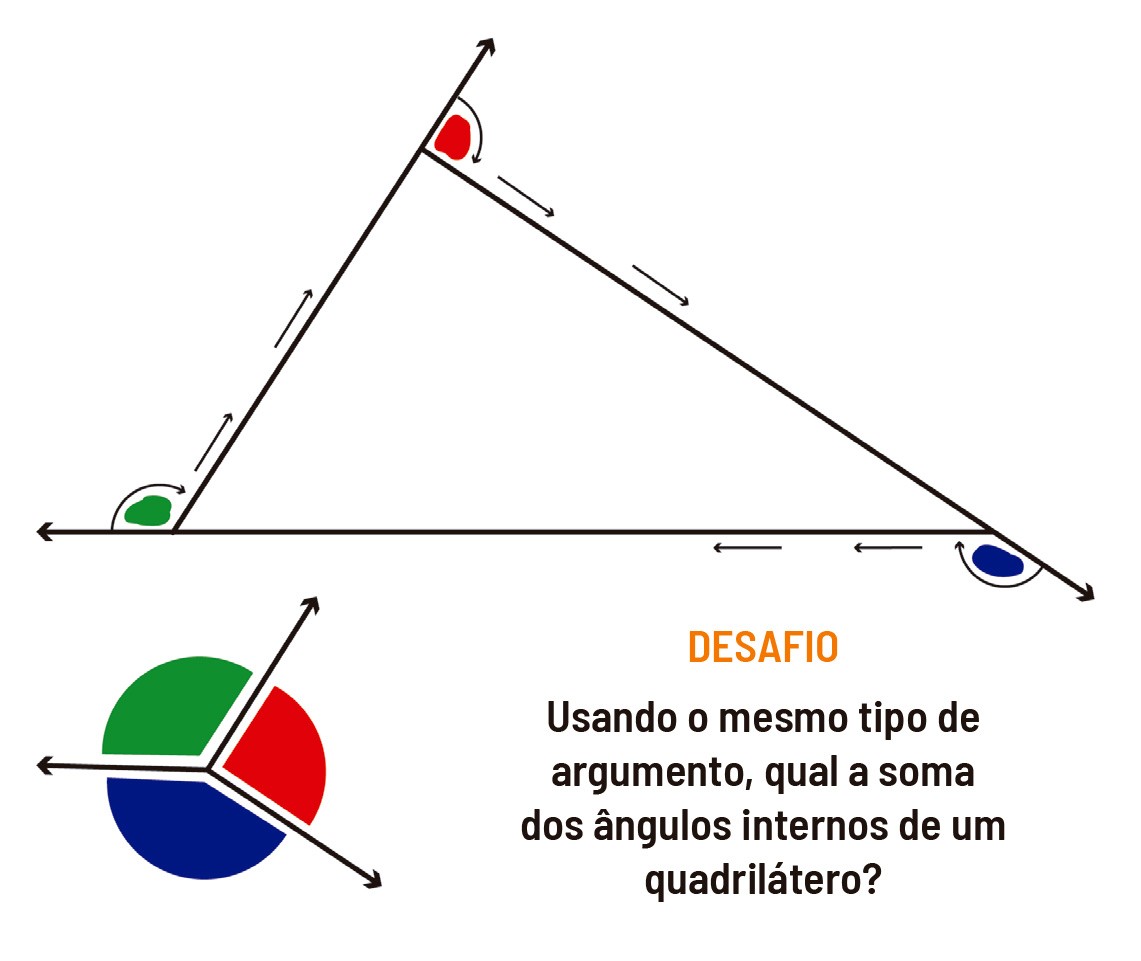
Vamos relembrar (ou antecipar!) uma lição básica da geometria: ‘a soma dos ângulos internos de um triângulo é 180 graus’. Talvez, você até se lembre da prova desse resultado com base em argumentos de geometria plana.
Provar resultados é fundamental na matemática. É o que nos dá segurança de que aquilo que estamos fazendo está correto. Mas, curiosamente, há uma diferença entre provar e entender. Exemplo: será que podemos entender por que a soma dos ângulos internos de um triângulo é 180 graus? Aliás, de onde vem a medida do ângulo?
Marco Moriconi
Instituto de Física,
Universidade Federal Fluminense
Para acessar este ou outros conteúdos exclusivos por favor faça Login ou Assine a Ciência Hoje.
Uma das vozes mais proeminentes na Colômbia sobre ecologia e desenvolvimento sustentável, a bióloga Brigitte Baptiste conta o que a natureza e a abertura à mudança podem ensinar à humanidade sobre a importância da diversidade e a construção de um mundo sustentável.
Problemas de contagem de coleções de objetos são parte de uma área da matemática chamada combinatória. Podem ser simples de explicar, mas requerem sutileza e engenhosidade em sua solução. Um estacionamento na frente de uma lojinha nos ajudará a apreciá-los
Os anos passam, mas Noel e seu ajudante Gunther continuam os mesmos! Deixam um presente que exige uma análise lógica interessante. Desta vez, a surpresa natalina inclui cinco caixas e um bilhete. No fim, apesar das ‘malandragens’ do Bom Velhinho, a visita acaba valendo a pena.
É possível saber se uma informação é verdadeira sem que nada seja revelado sobre ela? Dois amigos, uma caverna, uma palavra ‘mágica’ e um espião – somando-se a isso boa dose de ciência da computação e criptografia – mostram como responder a essa intrigante questão
